Une énigme classique demande de trouver quel élément est le plus lourd (ou le plus léger) parmi plusieurs en n’utilisant qu’un nombre limité de pesées. Par exemple :

8 pierres et une balance à 2 plateaux sont posées sur une table. Une des pierres est plus légère que les autres. Comment trouver de laquelle il s’agit en maximum 2 pesées ?

La balance s’utilise en plaçant sur chacun des plateaux un certain nombre de pierres : si les 2 plateaux restent à la même hauteur, alors leur contenu est de même poids ; au contraire, si un des plateaux descend (et donc que l’autre monte), cela signifie qu’un des contenus est plus lourd que l’autre (le plateau le plus bas sera le plus lourd). On comprend donc qu’il va falloir séparer les pierres en groupes, peser ces groupes, et en déduire laquelle est la plus légère.

On pourrait tester toutes les combinaisons - comme l'énigme La Traversée, mais contrairement à cette dernière, il y a plusieurs combinaisons dès le début : prendre 2 pierres au hasard, 4 pierres, séparer les 8 pierres en 2 groupes, voire mettre un nombre différent de pierres sur chaque plateau. Bref, ce serait trop long. Il va donc falloir comprendre comment utiliser au mieux la balance et les pierres.

Déterminer les informations récupérables

On pourrait penser qu’il faut séparer les pierres en 2 groupes, et que la balance nous permettra de déterminer lequel contient la pierre plus légère que les autres, mais il faut éviter ces raccourcis et se demander quelles sont toutes les informations qu’on peut récupérer de l’utilisation de la balance. Si on considère un plateau de la balance lors d’une pesée, il a en réalité 3 hauteurs possibles :

• Tout en bas → c’est le plus lourd, la pierre qu’on cherche est donc sur l’autre plateau

• Tout en haut → c’est le plus léger, la pierre qu’on cherche est sur ce plateau

• Au milieu → Les 2 plateaux pèsent autant, la pierre recherchée n’est pas sur les plateaux.

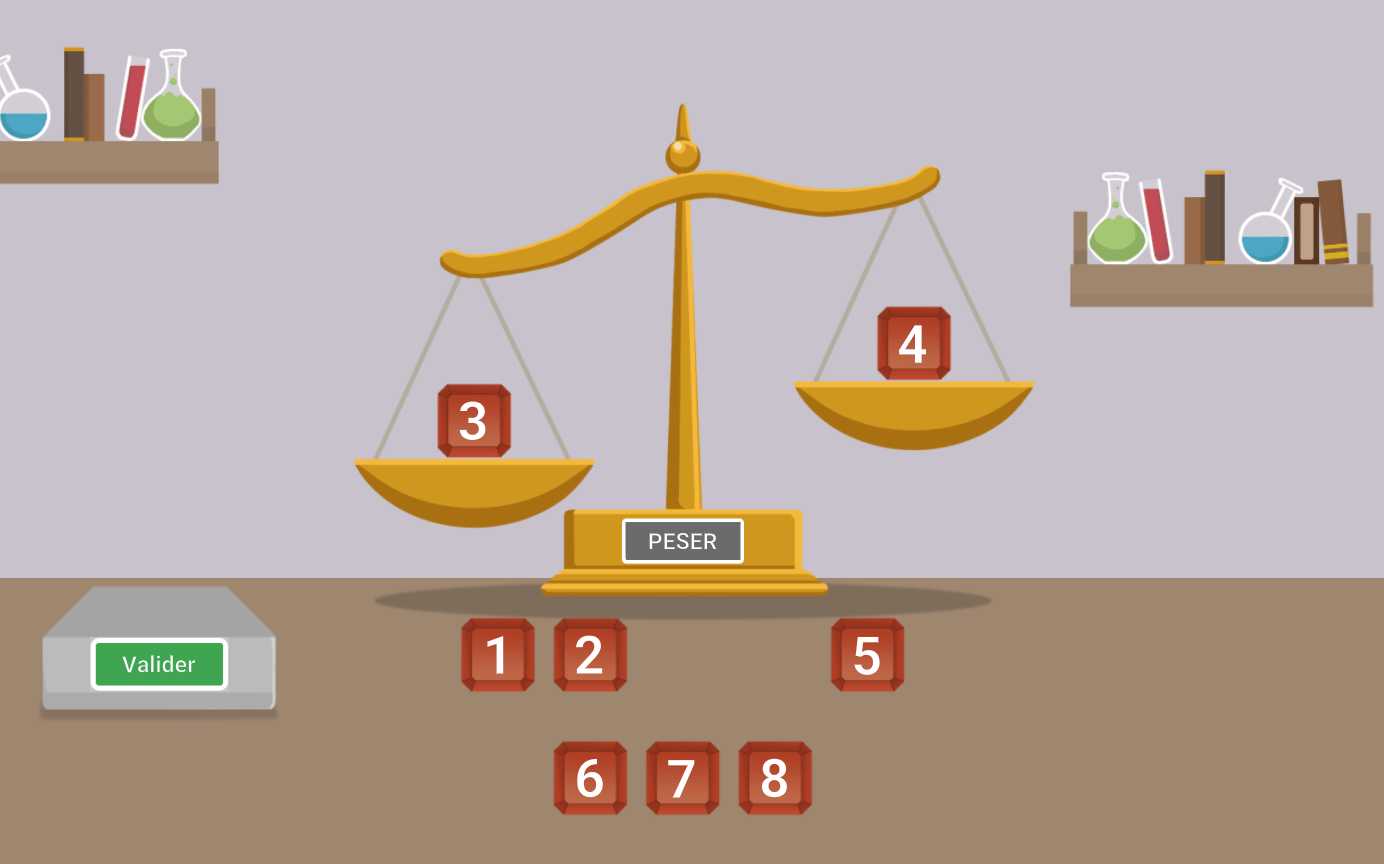
La balance permet donc de distinguer non pas seulement 2 mais 3 groupes, ce qui veut dire que pour éliminer les pierres, nous ne sommes pas obligés de faire 2 groupes, on peut aussi en faire 3. De plus, il y a une contrainte implicite que nous n’avons pas spécifiée : pour que l’information donnée par la balance soit pertinente, il faut placer le même nombre de pierres sur chaque plateau (sinon, le plateau avec le plus de pierre serait le plus lourd, mais on ne retirerait rien de cette information). Il faut donc également qu'au moins 2 groupes contiennent le même nombre de pierres. Pour déterminer le contenu de chacun des groupes, il nous manque cependant des informations.

Diviser pour mieux régner

Puisqu’on n’a le droit qu'à 2 pesées, on peut estimer que la résolution prendra 2 étapes :

1. Diviser les pierres, les peser, et en éliminer certaines
2. Diviser les pierres, les peser, et en déduire laquelle est plus légère.

Plutôt que de raisonner avec toutes les pierres et 2 pesées, une bonne méthode peut-être de commencer par la fin : de quoi a-t-on besoin pour réussir la deuxième étape ? Ou dit autrement : combien de pierres doit-il rester au maximum pour pouvoir déterminer laquelle est plus légère en une seule pesée ?

• S’il reste une pierre, c’est forcément la plus légère.
• S’il reste 2 pierres, on en met une sur chacun des plateaux et on regarde lequel monte.
• S’il en reste 3, on a vu dans la section précédente qu’on pouvait avoir la réponse, puisqu’il suffira de séparer en 3 groupes de 1 pierre, d’en peser 2, et la balance nous dira quelle pierre et plus légère : si l’un des plateaux bouge, la pierre sur le plateau le plus haut est plus légère ; si les plateaux restent à la même hauteur, alors les 2 pierres pèsent autant l’une que l’autre et la plus légère est donc la troisième, qu’on n’a pas pesée.
• S’il en reste 4 ? Si on en pèse 2 au hasard et que la balance reste droite, on saura que la pierre plus légère est dans les 2 restantes, mais on ne saura pas laquelle. Si on pèse les 4 (2 dans chaque plateau), on saura quel plateau est le plus léger mais on ne saura pas quelle pierre est la bonne. Si on ne met pas le même nombre de pierres dans chaque plateau, celui contenant le plus grand nombre de pierres sera forcément le plus lourd, ce qui ne nous apprendra rien.

On ne peut donc pas trouver la pierre la plus légère avec une seule pesée s’il en reste 4, mais on peut s’il en reste 3.

Regrouper les informations

Arrivé à ce stade, on sait qu’il faut 3 groupes maximum, et que chacun des groupes ne peut pas contenir plus de 3 pierres, car sinon on encourt le risque que la plus légère soit dans un groupe d’au moins 4 pierres, auquel cas on ne pourrait pas déterminer laquelle c’est en une seule pesée. Il faut donc faire maximum 3 groupes de maximum 3 pierres, et on n’oublie pas la contrainte de pesée : il faut qu'au moins 2 groupes contiennent le même nombre de pierres pour pouvoir les comparer. Ce groupement ne peut être fait que d’une seule façon :

• Si on forme 2 groupes contenant 1 seule pierre, le dernier groupe devrait contenir 6 pierres, or on ne peut pas dépasser 3 pierres par groupe.

• Si on forme 2 groupes de 2 pierres, le dernier groupe devrait en contenir 4, ce qui est trop.

• Si on forme 2 groupes de 3 pierres, le dernier groupe en contiendrait 2, ça fonctionne !

• On ne veut pas faire 2 groupes de 4 pierres, puisque ça dépasserait 3 pierres par groupe.

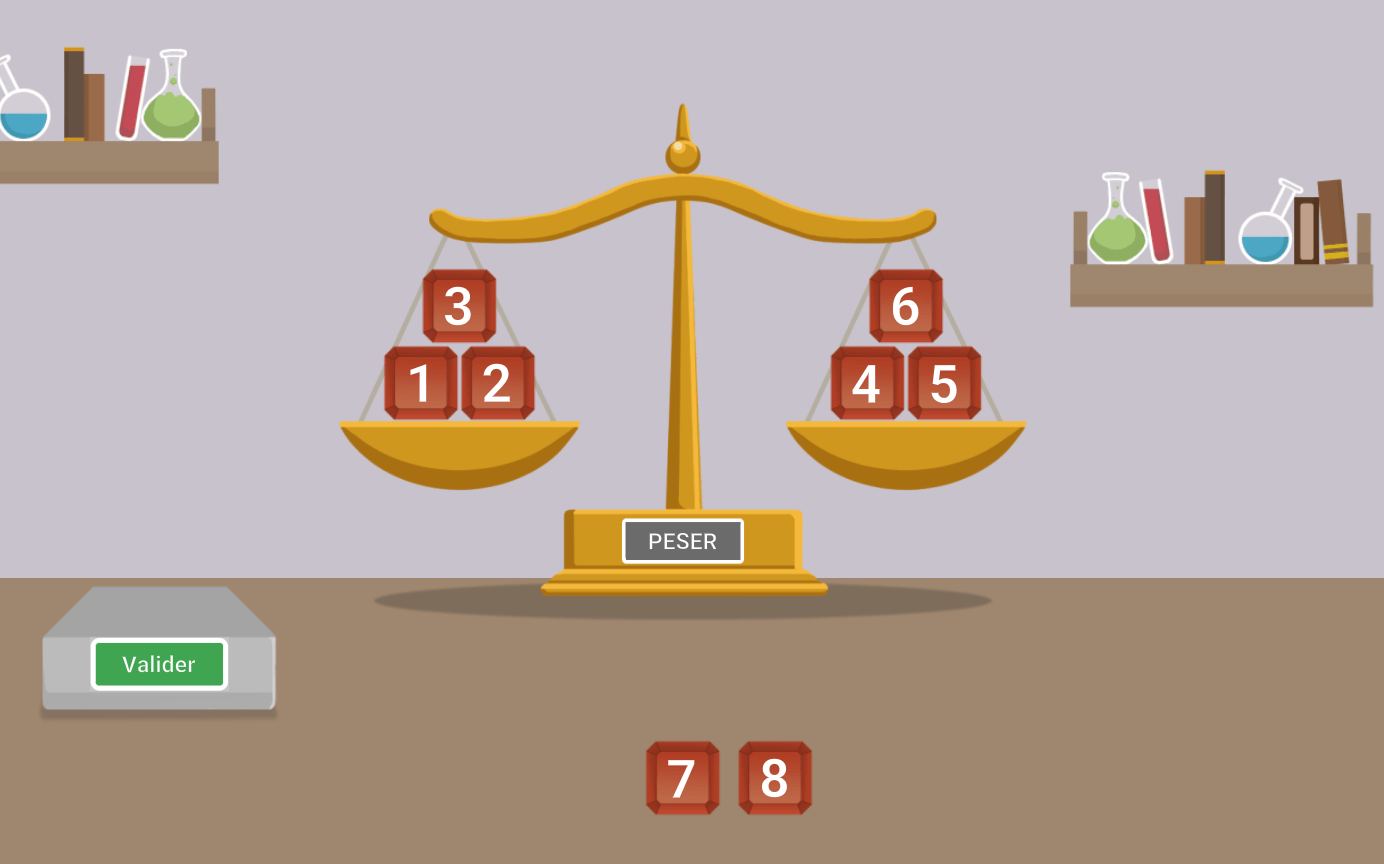
Ainsi le seul groupement possible est 2 groupes de 3 pierres et 1 groupe de 2 pierres.

Résoudre l'énigme

Puisque comparer 2 groupes de tailles différentes n’apporterait rien, la première étape est forcément de comparer les 2 groupes de 3 pierres.

• Si la balance reste stable, la pierre plus légère est dans le groupe qui n’a pas été pesé, composé de 2 pierres.

• Si la balance penche, la pierre que l’on cherche se trouve dans le plateau le plus haut, composé de 3 pierres.

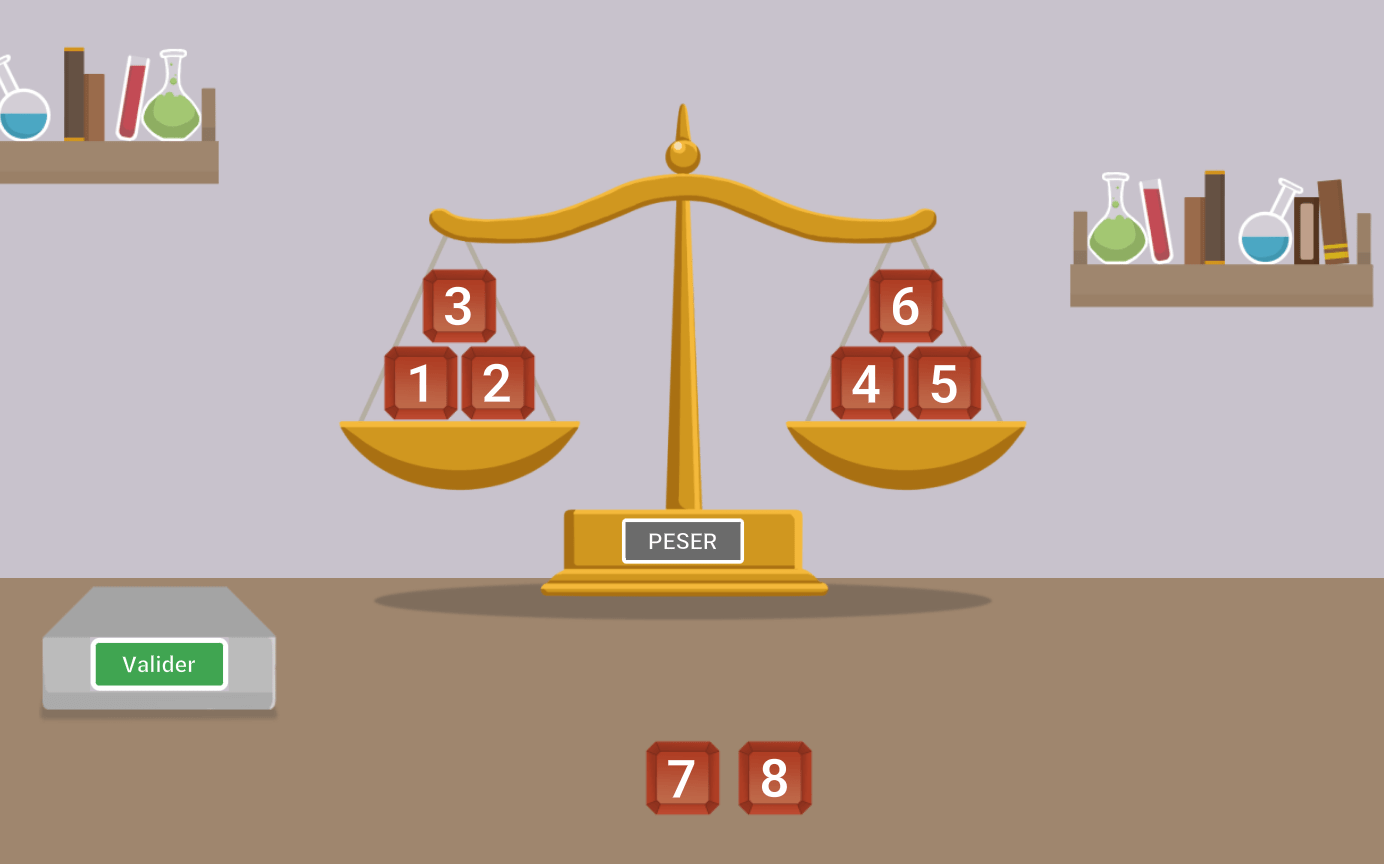
Ainsi pour la 2 seconde pesée, il ne nous reste plus que 2 ou 3 pierres, et nous avons vu dans la section diviser pour mieux régner comment déduire laquelle est la plus légère.

Vous pouvez explorer des énigmes similaires dans le jeu Bascule. Avec plusieurs niveaux à votre disposition, testez vos compétences à résoudre de telles énigmes et mettez en pratique les méthodes d'analyse que vous avez apprises.