Les explications données sur la fiche Bascule fonctionnent bien dans les cas les plus simples, mais si plutôt que de trouver la pierre la plus légère parmi 8 en 2 essais, on vous demandait de trouver la pierre différente (plus lourde OU plus légère) parmi 12 en 3 pesées, l’analyse des différentes combinaisons possibles serait trop longue pour être utilisable de manière raisonnable.

C’est là que cette fiche prend tout son intérêt : il existe un moyen de résoudre n’importe quel problème de ce type, et plus globalement tout problème dans lequel il faut trouver un intrus en récupérant une quantité finie d’informations sur plusieurs groupes d’éléments dont on peut choisir les états.

Le concept est d'assigner à chaque pierre une combinaison unique de résultats possibles lors de chaque pesée, et de vérifier à quelle pierre correspond les résultats réellement observés. Voyons comme réaliser ça !

Cas initial - L'énoncé indique que la pierre recherchée est plus légère (ou plus lourde)

On considérera que la pierre recherchée est plus légère pour illustrer, mais si dans votre cas elle est plus lourde, il suffira d’inverser le plateau ou les positionnements.

Définir les résultats possibles

Tout d’abord, il faut définir les résultats possibles pour une pesée. Pour cela, on va s’intéresser à un des plateaux (disons celui de gauche). Il peut être :

• En bas (indiquant soit qu’une pierre plus lourde est posée dessus, soit qu’une pierre plus légère est posée sur l’autre).
• En haut (indiquant soit qu’une pierre plus légère est posée dessus, soit qu’une pierre plus lourde est posée sur l’autre).
• Au milieu, indiquant que l’intrus n’est pas sur un des plateaux.

Assigner des combinaisons

Ensuite, on va attribuer une combinaison unique de résultats de pesées pour chacune des pierres. Il n’y a qu’une condition à respecter : il faut que pour chaque pesée, il y ait autant de pierres entraînant la levée du plateau que de pierres entraînant sa descente (sinon on ne pourra rien déduire de la pesée).

Par exemple :

Déduire les positionnements

On a choisi de s’intéresser au plateau gauche, et on cherche une pierre plus légère que les autres. Si la pierre posée sur le plateau gauche est plus légère, le plateau ira vers le haut, on va donc placer toutes les pierres attribuées à Haut sur le plateau de gauche, et celles attribuées à Bas sur le plateau de droite. Les pierres neutres ne seront pas pesées.

Observer les résultats

Il suffit ensuite de réaliser les pesées, et choisir la pierre correspondant aux résultats observés.

Exemple de procédure

Admettons que la pierre recherchée soit la 4 (on n’est pas au courant au début évidemment, mais il faut bien en choisir une pour illustrer).

Pour la première pesée, on place sur le plateau de gauche les pierres attribuées à Haut, c'est-à-dire les pierres 1, 4, 6 et 8, et on place sur le plateau de droite les pierres attribuées à Bas : les pierres 2, 5, 7 et 9. Le plateau de gauche va monter puisque la pierre 4 est plus légère.

On réalise ensuite la seconde pesée, en se basant sur le même principe : on regarde la ligne correspondant à la pesée #2, et on place à gauche les pierres assignées à Haut et à droite les pierres assignées à Bas. À gauche, on aura donc les pierres 1, 4, 8 et 12 ; à droite, les pierres 2, 5, 9 et 11. Le plateau de gauche va monter puisque la pierre 4 est plus légère.

On réalise enfin la troisième pesée : à gauche, les pierres 1, 9 et 10 ; à droite les pierres 2, 8, 12. Le plateau va rester neutre, car la pierre différente des autres (la #4) n’est pas sur un plateau.

Finalement, on regarde le tableau, et on cherche la pierre pour laquelle les positions du plateau de gauche sont Haut, Haut, puis Neutre, et on retombe bien sur la #4.

Cas général - On ne sait pas si la pierre recherchée est plus lourde ou plus légère

Quand on ne sait pas si la pierre est plus lourde ou plus légère, le raisonnement est assez différent bien que le processus soit similaire.

Résultats possibles

Les résultats possibles sont identiques au cas initial mais on ne peut pas en déduire la même chose. Pour s’en convaincre, imaginons que l’on pèse 2 pierres : on met la pierre #1 sur le plateau de gauche et la pierre #2 sur le plateau de droite ; à la pesée le plateau de gauche descend. Si on sait qu’on cherche la pierre la plus lourde, ce sera la #1 ; si on cherche la pierre la plus légère, ce sera la #2 ; si on ne sait pas si la pierre recherchée est plus lourde ou plus légère, quand le plateau descend on ne peut pas savoir si ça signifie que c’est la #1 qui est plus lourde que les autres ou si c’est la #2 qui est plus légère.

Assigner des positionnements

On ne peut certes pas déduire en une pesée si un groupe est plus léger ou si l’autre est plus lourd, mais on peut noter si le plateau sur lequel un groupe de pierres est posé est monté ou descendu, et on va utiliser cette information : on va assigner à chaque pierre une combinaison de plateaux, et il suffira de choisir la pierre que les pesées n’ont pas contredit. Par exemple, si l’on assigne les résultats suivants à une pierre :

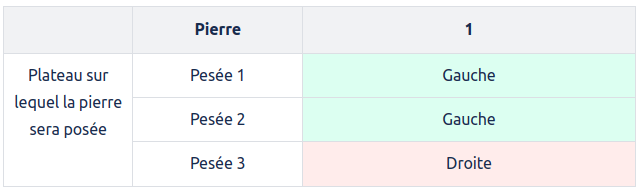
Qu’il monte ou qu’il descende, si le plateau de gauche bouge de la même façon les 2 première pesées que le plateau de droite à la 3ème pesée, alors la pierre #1 pourrait être l’intruse. Si par contre le plateau de gauche penche 3 fois du même côté, ou s’il reste neutre pour une des pesées, on saura à coup sûr que l’intruse n’est pas la pierre #1.

L’idée est donc de fixer à chaque pierre des combinaisons de manière à ce qu’après 3 pesées il n’y ait qu’une seule pierre qui puisse être la bonne.

Contrainte supplémentaire

Pour comprendre comment être sur qu’il ne puisse y avoir qu’un seul candidat après 3 pesées, il faut comprendre, étant donné un ensemble de résultats de pesées, quels seraient les candidats possibles. Pour cela, prenons un exemple : disons que sur la première pesée, le plateau de gauche descend (celui de droite monte donc), qu'à la 2ème pesée le plateau de gauche monte (celui de droite descend), et qu'à la 3ème pesée la balance reste neutre.

Si la pierre recherchée est plus lourde, elle aurait été placée d’abord à gauche (puisque le plateau de gauche descend à la première pesée), puis à droite (puisque c’est le plateau de droite qui descend pendant la 2ème pesée), puis elle n’aurait pas fait partie des pierres pesées (puisque les plateaux ne bougent pas) :

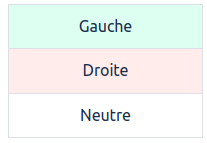
Si la pierre recherchée est plus légère, elle aurait été placée d’abord à droite (puisque le plateau de droite descend à la première pesée), puis à gauche pour la 2ème pesée, puis pas pesée du tout :

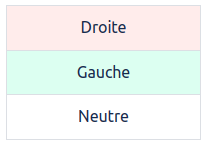
On ne sait pas si la pierre est plus lourde ou plus légère, donc si on avait ces 2 combinaisons, on ne pourrait pas savoir quelle pierre est la bonne. Par contre, on peut être sur que toutes les autres combinaisons sont incorrectes. Par exemple, si une pierre a la combinaison :

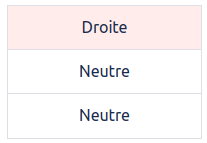
Elle ne peut pas être l’intruse car la balance n’est pas restée Neutre pendant la 2ème pesée alors que la pierre n’a pas participé à la pesée #2.

Dans la même idée, une pierre avec la combinaison :

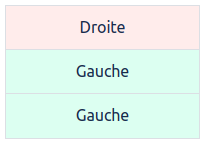
Cette pierre sera éliminée à la 3ème pesée car la balance reste Neutre alors que la pierre fait partie des pierres pesées.

On en déduit que les seules combinaisons qui peuvent se confondre sont celles pour lesquelles Droite et Gauche ont été inversés à chaque pesée (et les Neutre conservés). On ne peut par exemple pas avoir 2 pierres avec les combinaisons

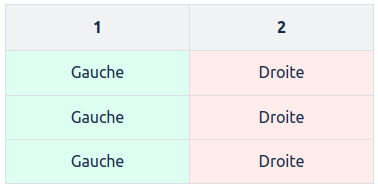
Un exemple valide de liste serait :

La création du tableau sera expliquée dans une future fiche. D’ici là, vous pouvez réutiliser ce tableau ou en créer un autre en y allant à tâtons.

Résolution

Pour chaque pesée, on va mettre toute les pierres assignées à gauche sur le plateau de gauche et sur le plateau de droite celles assignées à droite :

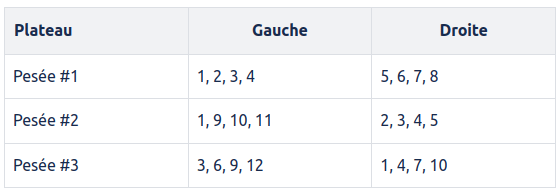
Admettons que la pierre #6 soit plus lourde que les autres :

• Lors de la première pesée, le plateau de gauche va monter et celui de droite descendre
• Lors de la seconde pesée, les plateaux vont rester neutre
• Lors de la troisième pesée, le plateau de gauche va descendre et celui de droite va monter
• On cherche donc la seule combinaison qui est neutre pour la pesée 2 et a des couleurs différentes pour les pesées 1 et 3 (puisque les plateaux n’ont pas eu le même comportement) :

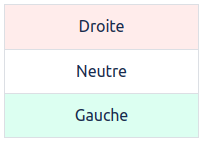
ou

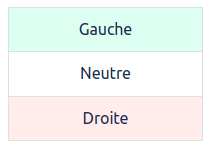
Et seule la pierre 6 correspond.

Autre exemple

Si on pèse les pierres dans le même ordre que l’exemple précédent, mais que la balance réagit différemment :

• Lors de la pesée 1, le plateau de gauche descend
• Lors de la pesée 2, le plateau de gauche monte
• Lors de la pesée 3, le plateau de gauche monte

De quelle pierre s'agit-il ?

Eh bien on va regarder dans notre tableau quelle pierre a des couleurs à chaque ligne (puisque les plateaux ne sont jamais restés neutres), avec la couleur associée à la pesée 1 différente de la couleur des pesées 2 et 3 (puisque la balance a eu le même comportement pour les pesées 2 et 3 et un comportement différent pour la pesée 1. Les solutions possibles sont donc :

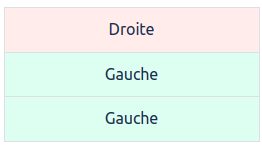
ou

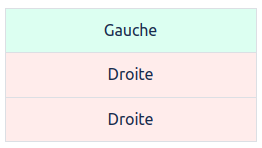
Et seule la pierre #4 correspond.